?sin60度(sin60度的三角函數值)
sin60度(sin60度的三角函數值)
老黃覺得,解三角形最重要的三個公式分別是:正弦公式、余弦公式和三角形的正弦面積公式,以及它們的變形公式。2022年新高考全國卷II的解三角形問題,就很好地結合了這三個重要公式。
記△ABC的內角A, B, C的對邊分別為a, b, c, 以a, b, c為邊長的三個正三角形的面積分別S1, S2, S3, 且S1-S2+S3=√3/2, sinB=1/3.
(1)求△ABC的面積.
(2)若sinAsinC=√2/3, 求b.
原題是沒有圖形的,老黃為了做個封面,就畫了下面的圖形,也能更直觀地理解題目的條件和要求。我個你講喔,要把這個圖畫準確,可比解這道題難多了哦。當然老黃也就畫個草圖而已。
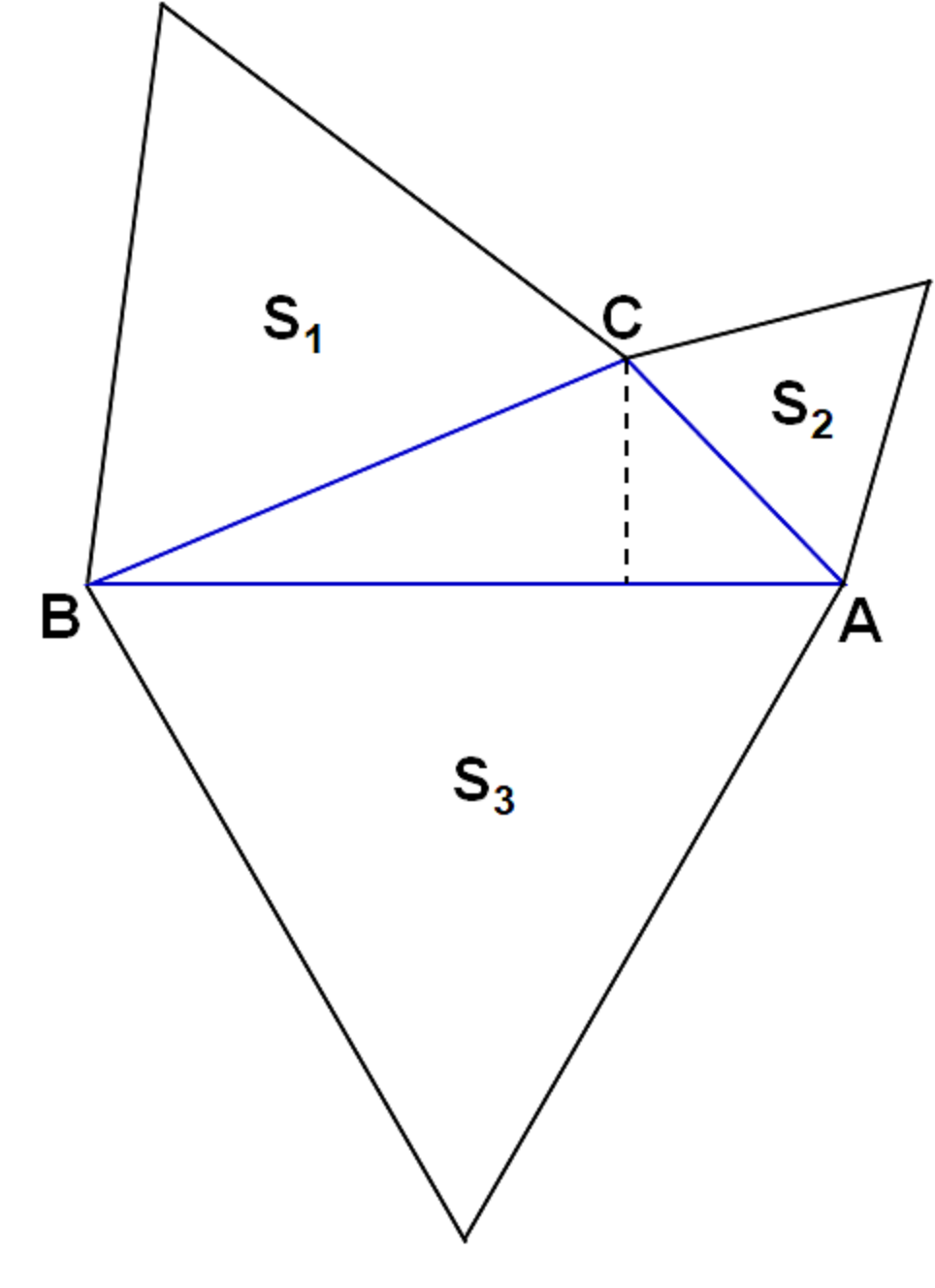
分析:(1)題目的突破點之一,是利用三個正三角形的正弦面積公式,即S1=a^2sin60度/2, S2=b^2sin60度/2, S3=c^2sin60度/2, 利用題目所給的三個正三角形的面積關系,就可以轉化得a^2-b^2+c^2=2. 因為上面所提到的三個公式都與邊角有關,所以把面積關系轉化成邊的關系,會有更多的可能。
接下來利用角B的余弦公式:2accosB=a^2+c^2-b^2,就可以得到accosB=1.
下面判斷角B是銳角還是鈍角,因為要用到它的余弦,所以要判斷角B的余弦的符號性質。因為b^2=a^2+c^2-2,即b比直角三角形勾股定理中的斜邊相對要小,根據“小邊對小角”,可以知道,角B是一個銳角。
因此cosB=√(?( )^)=2√/3, 這就可以求得ac=1/cosB=3√/4.
再次運用三角形ABC的正弦面積公式,就有S△ABC=acsinB/2=√/8.
(2)第二小題一看就知道要用到正弦公式:sinA/a=sinB/b=sinC/c. 然后分別用邊的關系表示sinA和sinC. 就有邊角關系sinAsinC=ac/(9b^2). 分子分母同時乘以cosB, 分子化為accosB=1,分母則化為9b^2cosB=6√b^2. 即1/(6√b^2)=√/3. 輕松解得b=1/2, 或b=-1/2(舍去).
下面組織解題過程:
解:(1)S1-S2+S3=(a^2-b^2+c^2)sin60度/2=√3/2,
a^2-b^2+c^2=2, 又a^2+c^2-b2=2accosB, ∴accosB=1,
由b^2=a^2+c^2-2, 知B<90度. cosB=√(1-(sinB)^2)=2√2/3,
△ABC的面積S=acsinB/2=ac/6=1/(6cosB)=√2/8.
(2)由sinA/a=sinB/b=sinC/c,有sinA=a/(3b), sinC=c/(3b).
sinAsinC=ac/(9b^2)=1/(9b^2cosB)=1/(6√2b^2)=√2/3.
解得: b=1/2, 或b=-1/2(舍去).
所以,解三角形的三個重要公式及其各種變形形式,你都掌握了嗎?
-

- ?微信視頻號可以屏蔽別人嗎(微信視頻號可以屏蔽別人嗎怎么設置)
-
2024-01-31 13:14:53
-

- ?紅富士蘋果產地在哪里(山西紅富士蘋果產地在哪里)
-
2024-01-31 13:12:38
-

- ?海賊王連載了多少年了(海賊王連載具體時間)
-
2024-01-31 13:10:24
-
- ?飛行模式別人打電話會怎么樣(飛行模式鬧鐘會響嗎)
-
2024-01-31 13:08:09
-
- ?堵車的句子經典語句(堵車的句子經典語句圖片)
-
2024-01-31 13:05:54
-
- ?除氯是什么意思(恒溫水壺除氯功能是干嘛的)
-
2024-01-31 13:03:40
-
- ?七七事變盧溝橋在哪個城市(盧溝橋七七事變是在哪個城市)
-
2024-01-29 06:13:47
-

- ?黑膚色適合什么顏色衣服(黑膚色適合什么顏色衣服顯白夏天)
-
2024-01-29 06:11:33
-
- ?oppo怎么截屏幾種方法(oppo怎么截屏的oppo手機怎樣截屏)
-
2024-01-29 06:09:18
-
- ?學信網密碼忘了手機號換了怎么辦(學信網密碼忘了手機號換了怎么辦學信網)
-
2024-01-29 06:07:03
-

- ?汪汪隊主題歌(汪汪隊主題歌曲中文版歌詞)
-
2024-01-29 06:04:48
-
- ?民用天然氣多少錢一立方(民用天然氣多少錢一立方米)
-
2024-01-29 06:02:34
-
- ?精誠團結是什么(精誠團結是什么生肖)
-
2024-01-29 06:00:19
-

- ?電腦截屏最快的方法(電腦截屏最快的方法是什么)
-
2024-01-29 05:58:04
-

- ?蔥油拌面的做法(上海蔥油拌面的做法)
-
2024-01-29 05:55:50
-
- ?笑到抽筋的十大極品幽默笑話(笑到抽筋的笑話 史上最強)
-
2024-01-29 05:53:35
-
- ?微信鈴聲下載(微信鈴聲下載免費)
-
2024-01-29 05:51:20
-

- ?木加一筆變新字(木加一筆變新字6個)
-
2024-01-29 05:49:06
-
- ?巨蟹男瘋狂愛上一個人的表現(巨蟹男瘋狂愛上一個人的表現是什么)
-
2024-01-29 05:46:51
-
- ?安卓區的王者榮耀怎么轉到蘋果區(安卓區的王者榮耀怎么轉到蘋果區免費)
-
2024-01-29 05:44:36



 ?為什么說俄烏戰爭:俄軍傷亡比烏軍更多!俄烏大戰將在2023年結束
?為什么說俄烏戰爭:俄軍傷亡比烏軍更多!俄烏大戰將在2023年結束