12和8的最大公因數是多少（12和8的最大公因數是多少最小公倍數是多少）

12和8的最大公因數是多少（12和8的最大公因數是多少最小公倍數是多少）

五年級重點內容，公因數的學習需要在整除的基礎上進行學習，首先得知道什么是因數，a數能被b數整除，那么b就是a的因數。

幾個數公有的因數，叫作這幾個數的公因數，其中最大的一個叫作這幾個數的最大公因數。我們可以把自然數a，b的最大公因數記作(a，b)，如果(a，b)＝1，則a和b互質。可以用短除法求出幾個數的最大公因數。短除法估計大家都會用，我就不再重復了。下面看幾個巧用公因數的常見題目。

難題點撥

把一張長12厘米、寬8厘米的長方形紙裁成相同的正方形紙片(紙沒有剩余)，至少能裁成多少片?

解題分析：這個題目是最典型的一個公因數題目，要求裁的片數最少，那么每片小正方形的邊長就得最大，很顯然是求最大公因數的。讀題，把長12厘米、寬8厘米的長方形紙裁成相同的正方形紙片，要求紙沒有剩余，那么裁成的小正方形紙片的邊長應該是12厘米和8厘米的公因數，因為要求至少裁成多少片，所以小正方形紙片的邊長應該是12厘米和8厘米的最大公因數。

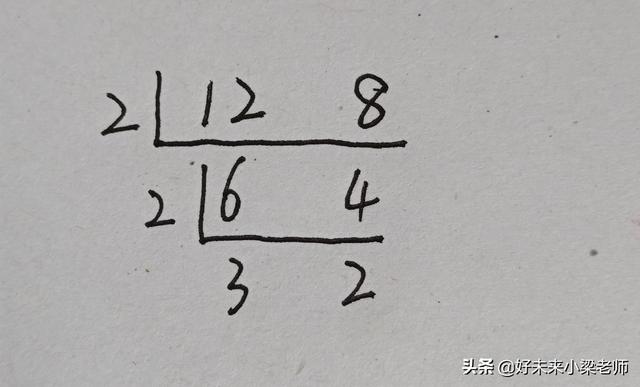
12和8的最大公因數是2×2＝4，所以裁成的小正方形紙片的邊長是4厘米。

沿著長方形紙的長可以裁成:12÷4＝3(片)

沿著長方形紙的寬可以栽成:8÷4＝2(片

這張長方形紙一共可以裁成:3×2＝6(片)

答：至少能裁成6片。

難題點撥

將一個長105厘米、寬45厘米、高30厘米的長方體木料，鋸成同樣大小的小正方體，如果不計損耗，鋸完后木料不許有剩余，鋸成的小正方體木塊的棱長是大于1厘米的自然數。可以有幾種不同的鋸法?每種鋸法中小正方體的棱長是多少?分別可以鋸成多少塊?

解題分析：分析題目中的條件，我們可以知道，鋸成的小正方體木料的棱長應該是長方體木料長、寬、高的公因數(除1以外)。

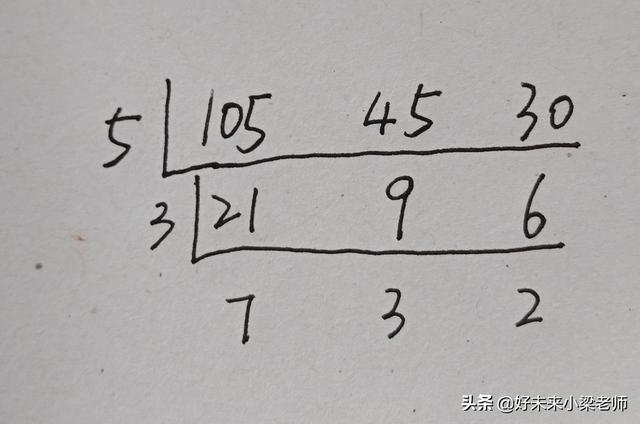
105，45和30除1以外的公因數有5，3和3×5＝15。

因此，可以有三種不同的鋸法：

鋸成的小正方體木料的棱長是5厘米，可以鋸成(105÷5)×(45÷5)×(30÷5)＝1134(塊)

鋸成的小正方體木料的棱長是3厘米，可以鋸成(105÷3)×(45÷3)×(30÷3)＝5250(塊)

鋸成的小正方體的棱長是5×3＝15(厘米)，可以鋸成(105÷15)×(45÷15)×(30÷15)＝42(塊)

答:可以有三種不同的鋸法。鋸成的小正方體的棱長是5厘米，可以鋸成1134塊；鋸成的小正方體的棱長是3厘米，可以鋸成5250塊；鋸成的小正方體的棱長是15厘米，可以鋸成42塊。

難題點撥

有三根小棒，分別長12厘米、44厘米、56厘米。要把它們截成同樣長的小棒，不許有剩余，每根小棒最長能有多少厘米?一共可以截成多少根小棒?

解題分析：這道題實際是求12，44和56的最大公因數，用短除法求出這三個數的最大公因數。

12，44和56的最大公因數是:2×2＝4

因此，每根小棒最長是4厘米。

長12厘米的小棒可以截成3根，長44厘米的小棒可以截成11，長56厘米的小棒可以截成14根，一共可以截成3+11+14＝28(根)

答:要把它們截成同樣長的小棒，不許有剩余，每根小棒最長是4厘米，一共可以截成28根小棒。

難題點撥

幼兒園阿姨給小朋友分蘋果，如果把167個蘋果平均分給小朋友，還剩下5個；如果把111個蘋果平均分給小朋友，還剩下3個；如果把66個蘋果平均分給小朋友，還剩下12個。請你算一算，幼園最多有多少個小朋友?

解題分析：根據題中的條件，如果把167－5＝162(個)蘋果平均分給小朋友，應該剛好分完，沒有剩余；同樣，如果把111－3＝108(個)蘋果平均分給小朋友，也應該剛好分完，沒有剩余；把66-12＝54(個)蘋果平均分給小朋友，也應該剛好分完，沒有剩余。

這樣，幼兒園的小朋友數應該是162，108和54的公因數，又因為求“最多有多少個小朋友”，所以就是求162，108和54的最大公因數。108和54的最大公因數是54，所以幼兒園最多有54個小朋友。

答:幼兒園最多有54個小朋友。

難題點撥

一個林場有男職工96人，女職工72人，在一次勞動中分成小組，要求每個小組的男職工人數相等，女職工人數也相等。最多能分成多少個小組?每個小組最少有多少人?

解題分析：題中男職工96人，女職工72人，分組，要求分的組最多，也就是求96和72的最大公因數，用短除法求出最大公因數是2×2×2×2×3＝24，也就是最多可以分24個組。

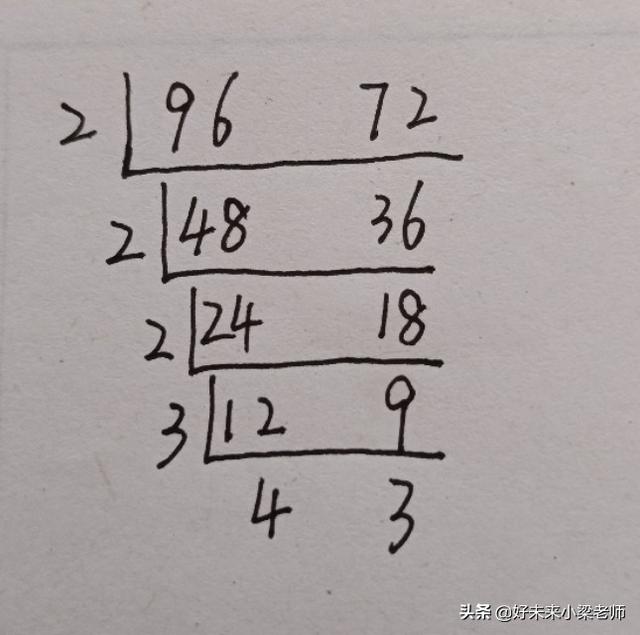
每組有男職工：96÷24＝4人

每組有女職工：72÷24＝3人。

答：最多可以分成24組，每組最少有男職工4人，女職工3人。

難題點撥

兩個兩位數的乘積是1734(兩個數不是倍數關系)，它們的最大公因數是17。求這兩個數。

解題分析：這個題目中我們可以設這兩個數分別是a×17和b×17。由題中條件可以列出以下關系式：

(a×17)×(b×17)＝1734

a×b＝1734÷17÷17＝6

因為a，b兩個數不存在倍數關系，所以a＝2，b＝3。那么a×17＝34，b×17＝51。

答：這兩個數分別是34和51。

1.一張長方形紙，長是32分米，寬是12分米，要把它裁成面積最大的小正方形紙片，而且不能有剩余，裁成的小正方形紙片的面積是多少平方分米?可以裁成多少片?

2.一塊長方形玻璃，長是12分米，寬是8分米，要把它裁成同樣大小的小正方形玻璃(邊長均為整分米數)，不許有剩余，不計損耗。裁成的小正方形玻璃的邊長是多少?可以裁成多少塊?

3.一個長方體木塊，長是2.7分米，寬是1.8分米，高是1.5分米。要把它鋸成大小相等的小正方體木塊，不許有剩余，小正方體木塊的棱長最大是多少分米?

4.一根長方體木料，長是105厘米，寬是63厘米，高是42厘米，鋸成同樣大小的小正方體，如果不計損耗，鋸完后木料不許有剩余，鋸成的小正方體木塊的棱長是大于1厘米的自然數。可以有幾種不同的鋸法?每種鋸法中小正方體的棱長是多少?分別可以鋸成多少塊?

5.一塊長54厘米、寬27厘米、高18厘米的長方體鐵塊，要切割成同樣大小的小正方體，如果不計損耗，切割完后鐵塊不許有剩余，切割成的小正方體鐵塊的棱長是大于1厘米的自然數。可以有幾種不同的切割方法?每種切割方法中小正方體的棱長是多少?分別可以切割成多少塊?

6.有一根長方體木料，長是120厘米，寬是40厘米，高是20厘米，如果要把這根木料鋸成棱長是10厘米的小正方體，可以鋸成多少塊?

7.有三根鋼管，它們的長度分別是240厘米、200厘米、320厘米，如果把它們截成同樣長的小段，每小段最長可以是多少厘米?

8.有三根木料，分別長12分米、18分米、24分米，把這三根木料分別截成同樣長的小段，每小段木料最長是多少分米?一共可以截成多少段?

9.某市有一個三角形公園，三邊長分別為498米、612米、582米。計劃每隔若干米植一棵松樹，并且每相鄰兩棵之間的距離要最遠。問:至少要植松樹多少棵?

10.一個數，不知道是多少，56除以它余2，110除以它余2，138除以它余3。這個數最大是多少?

11.美術老師買了一些鉛筆，打算把它們平均分給美術小組的同學們，拿54支鉛筆來分，結果余下了3支，拿70支鉛筆來分，結果余下了2支。你能知道這個美術小組有多少個學生嗎?

12.用某數去除600余5，去除813余8，去除844余4。這個數最大是多少?

13.把一個棱長是12厘米的正方體木塊分割成棱長是4厘米的小正方體，可以分多少塊?

14.有兩種鋼筋，第一種長180厘米，有6根；第二種長240厘米，有1根。現在要鋸成每段最長且相等的小段，不能浪費鋼筋，一共可以鋸成多少段?

15.上海路中學召開代表大會，有教師代表32人，學生代表40人，職工代表24人，要編成若干組進行討論，編組時各方代表人數要相等，最多能編幾組?每組有各方代表各幾人?

16.ー條道路由甲村經過乙村到丙村。已知甲、乙兩村相距120米，乙、丙兩村相距125米。現在準備在甲、丙兩村之間的路的兩邊栽上柳樹，并且在甲、乙、丙三個村子的村口都要栽上樹，要求相鄰兩棵樹之間的距離相等。問:一共可以栽多少棵樹？

17.有339個蘋果、259個梨子、214個橘子，正好分成每份同樣多的禮物后，草果多3個，梨子多7個，橘子多4個，這些水果最多可以分成多少份同樣的禮物?在每份禮物中，三種水果各有多少個?

18.工人加工了三批零件，每加工一批零件，除了王師傅比其他工人多加工若干個外，其他工人加工的都同樣多。已知他們第一批共加工2100個，其中王師傅比每個工人多加工7個;第二批加工1800個，其中王師傅比每個工人多加工6個;第三批加工1600個，其中王師傅比每個工人多加工13個。這批工人最多有多少人?

所有題目答案如下：

1.16平方分米，24片

2.有三種不同的裁法。

第一種:如果裁成的小正方形的邊長是1分米，可以裁成(12÷1)×(8÷1)＝96(塊);

第二種:如果裁成的小正方形的邊長是2分米，可以裁成(12÷2)×(8÷2)＝24(塊);

第三種:如果裁成的小正方形的邊長是4分米，可以裁成(12÷4)×(8÷4)＝6(塊)。

3、0.3分米

4、可以有三種不同的鋸法。

第一種：小正方體的棱長是3厘米，可以鋸成(105÷3)×(63÷3)×(42÷3)＝10290(塊)

第二種：小正方體的棱長是7厘米，可以鋸成(105÷7)×(63÷7)×(42÷7)＝810(塊)

第三種：小正方體的棱長是3×7＝21(厘米)，可以鋸成(105÷21)×(63÷21)×(42÷21)＝30(塊)。

5、有兩種不同的切割方法。

第一種：棱長3厘米，可以切割成(54÷3)×(27÷3)×(18÷3)＝972(塊)

第二種:棱長3×3＝9(厘米)，可以切割成

(54÷9)×(27÷9)×(18÷9)＝36(塊)。

6、(120÷10)×(40÷10)×(20÷10)＝96(塊)

7、40厘米

8、6分米，12÷6+18÷6+24÷6＝9(段)

9、282棵

10、27

11、17個

12、35

13、(12÷4)×(12÷4)×(12÷4)＝27(塊)

14、22段

15、(32，40，24)＝8(組)，每組中教師有32÷8＝4(人)，學生代表有40÷8＝5(人)，職工代表有24÷8＝3(人)

16、100棵

17、339－3＝336(個)。

259－7＝252(個)，

214－4＝210(個)

(336，252，210)＝42(份)

每份中，蘋果:336÷42＝8(個)，

梨:252÷42＝6(個)，

橘子:210÷42＝5(個)

18、

2100－7＝2093(個)

1800－6＝1794(個)

1600－13＝1587(個)

(2039，1794，1587)＝23

答：這批工人最多有23人。